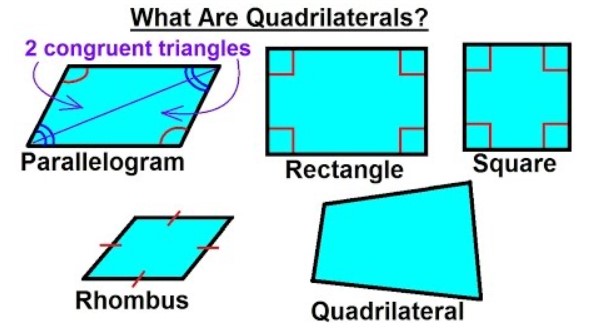
There are various geometrical shapes in mathematics, one of them is the ‘Quadrilateral’. It is a closed figure which is bounded by 4 sides that are non-collinear to each other. Any three sides of a quadrilateral can be non-collinear. It has been derived from the words of Latin which signifies four sides. It is inclusive of 4 sides, angles and vertices respectively.
These four sides of the quadrilateral can be equal or cannot be equal to each other. A quadrilateral is bounded by sides namely, ABCD where four sides are, AB, BC, DA, and CD. It also contains 2 diagonals namely, AC and BD. Each angle measures around 90 degrees.
Therefore, the sum of all the interior angles measures around 360 degrees. It has been categorized into various categories based on the properties such as square, rectangle, parallelogram, rhombus, and so on. In this article, we shall cover some basic topics related to quadrilaterals like the area of quadrilaterals, properties, and some examples related to them.
Table of Contents
Area of Quadrilateral
A quadri lateral can be considered as an irregular or a regular shape. The area of any shape can be defined as the total space occupied inside it. Similarly, the area of a quadrilateral can be considered as the total square units of space or region which are occupied within a quadrilateral.
The area of a quadrilateral can be calculated using various ways such as: using sides, using the heron’s formula, and many more. But, the most common way is by using the help of sides and heights of the quadrilateral. It is divided into triangles.
The mathematical formula to calculate the area of quadrilateral using sides and height is, ½ * d * (height 1 + height 2) where ‘d’ is the diagonal of the triangles. You must remember that the resultant value is always written in a unit square. For example, cm unit square or meter unit square. We shall solve some examples related to it in the next section.
Some Important Properties of a Quadrilateral
As mentioned above, a quadrilateral is a closed figure which is bounded by 4 sides that are non-collinear to each other. As with every other shape, it also comprises its property which makes it different from other shapes. The following points mentioned below analyze those distinctive properties of a quadrilateral.
- A quadrilateral consists of three collinear points.
- It includes 4 sides, vertices, and angles respectively, and two diagonals.
- Each angle measures about 90 degrees. Thus the sum of 4 angles is equivalent to 360 degrees. ( 90 + 90 + 90 + 90 = 360 ) .
- A quadrilateral is categorized into various types. Some of them are as follows: rectangle, square, rhombus, kite, parallelogram, and so on.
Examples Based on the Area of Quadrilateral
Till now, you may have understood the shape: quadrilateral. The mathematical formula to calculate the area of quadrilateral using sides and height is, ½ * d * (height 1 + height 2) where ‘d’ is the diagonal of the triangles. Let us now solve some examples related to the area of quadrilaterals. Some examples are listed below:
Example 1:
calculate the area of quadrilateral if the diagonal is 7 cm and height 1 and height 2 is equivalent to 3 and 4 cm respectively?
Solution: Given that,
Diagonals of the quadrilateral = 7 cm
Height 1 of the quadrilateral = 3 cm
Height 2 of the quadrilateral = 4 cm
Using the formula of the area of quadrilateral = ½ * d * ( height 1 + height 2 ).
½ * 7 * ( 3 + 4 ) = ½ * 7 ( 7 ).
½ * 7 ( 7 ) = ½ * 7 * 7.
½ * 49 = 0.5 * 49.
0.5 * 49 = 24.5 cm unit square. Hence, the area of quadrilateral for the given height and diagonal is = 24.5 cm unit square.
You can study the concept of quadrilaterals in an interactive way by visiting Cuemath.
Visit for more articles